Saviez-vous que vous rencontrez plus régulièrement des nombres qui commencent par le chiffre « 1 » que des nombres qui commencent par le chiffre « 9 » ? Ce résultat surprenant fait l’objet de nombreuses publications mais n’est pas encore largement dans le monde de l’entreprise. Pourtant, à l’heure du tout digital, cette loi constitue un outil intéressant pour lutter contre les falsifications des données dans le traitement numérique de masse. Après une introduction théorique et jalonnée d’exemples, on expliquera comment tester concrètement vos données avec l’aide d’un fichier Excel en décrivant certaines bonnes pratiques d’utilisation. Prêt, feu, partez !
La loi de Benford
Énoncée simplement elle stipule que dans une liste numérique quelconque, si vous regroupez les nombres selon leur premier chiffre significatif, vous en dénombrerez plus qui commencent par « 1 » que par « 2 » que par « 3 » et ainsi de suite jusqu’à « 9 ».
Par exemple : le registre des amortissements des biens de la ville de Paris – accessible en Open Data – dénombre plus de 40 000 valeurs de biens à l’achat avec un montant exprimé en euros. En analysant cet échantillon de données, j’ai pu mettre en évidence les fréquences d’apparitions du premier chiffre significatif comme suit :
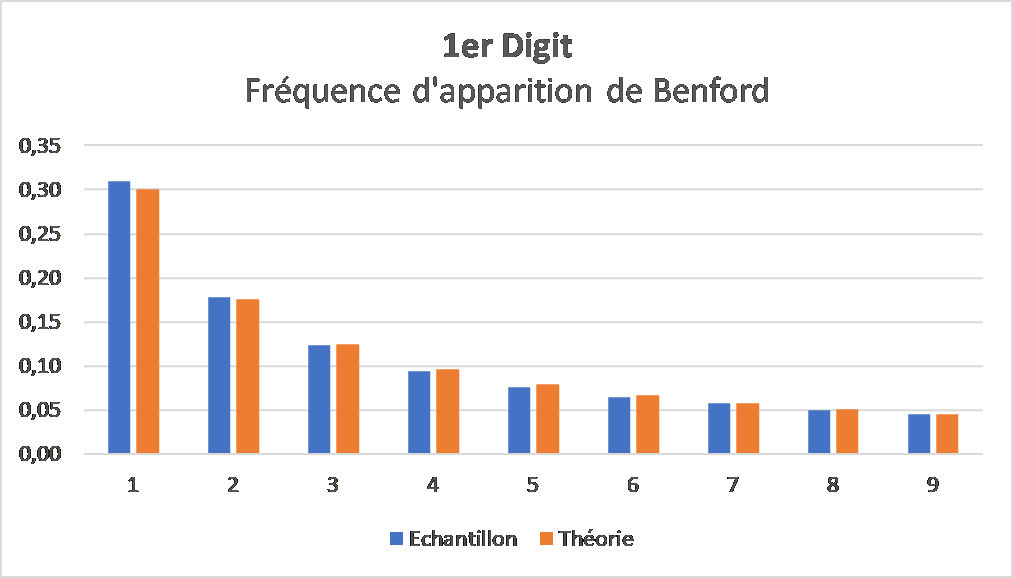
Analyse de Benford des acquisitions de la ville de Paris par rapport à la loi statistique théorique, opendata.paris.fr – décembre 2017
Ce qui frappe c’est que ces fréquences semblent strictement décroissantes alors que notre intuition suggère qu’elles devraient être uniformes : on en veut pour preuve les nombres générés aléatoirement par l’informatique qui sont équiprobables. Pourtant, il ne s’agit pas d’un biais de l’échantillon mais bel et bien d’un phénomène de fond connu sous le nom de son codécouvreur : la loi de Benford. Des études portant sur des milliards de données diversifiées (mathématiques, géographiques, financières etc) ont montré que que ce résultat de Benford est persistant. Si la loi fut d’abord empirique, il est maintenant prouvé qu’elle est rigoureusement vraie pour certains types de données. On l’exprime par la formule suivante :
P(c) = Log10(1 + c/10) avec c pour le premier chiffre significatif à prendre parmi {1,2,3,4,5,6,7,8,9} et P(c) la probabilité associée à sa fréquence d’apparition.
Faites l’expérience suivante : prenez un journal au hasard, ouvrez une page au hasard et relevez le premier nombre contenu dans la page. Vous aurez environ Log10(1 + 1/10) ≈ 30% de chance qu’il commence par un « 1 » et seulement Log10(1 + 9/10) ≈ 4,5% de chance qu’il commence par un « 9 ». Ce résultat est si étonnant que l’on voit tout de suite le potentiel d’un jeu de hasard exploitant ce résultat 😉
Dans cette loi, il existe aussi une formulation de second niveau qui porte sur les k-ème chiffres significatifs. La probabilité devient quasiment équilibrée dès la 4ème décimale. En d’autres termes un « 1 » a quasiment autant de chance d’apparaitre qu’un « 9 » dès que l’on avance dans la composition d’un nombre dans sa forme canonique.
Des propriétés singulières
La propriété la plus remarquable est que loi de Benford est indépendante de la mesure. En d’autres termes, si l’on compile des données financières exprimées en euros et qui suivent la loi de Benford, la transformation de ces données dans une autre devise suivra également la loi ! Pour les curieux, il existe une démonstration simple de l’invariance par la multiplication.
Autre conséquence : la loi reste valable indépendamment de la base numérique choisie. Dire que l’on suit cette loi dans la base 6 – communément utilisée dans le système heure, minute, seconde – revient à la probabilité donnée par la formule P(c) = Log6(1 + c/6). Bref, la distribution reste « de Benford » si l’on décide de convertir des données dans n’importe quelle autre base !
Pour en savoir davantage sur l’aspect mathématique, je vous conseille l’article de Jean-Paul DELAHAY (Pour La Science 351, décembre 2006) ou le billet d’Elise Janvresse sur le blog Images des mathématiques (CNRS). La page anglaise de Wikipedia sur le sujet contient également quelques informations complémentaires à ce sujet.
Pour l’heure on va souffler un peu et revenir à un domaine plus terre-à-terre…
Benford par la pratique : la détection de fraudes
Pendant des années ce résultat est resté une curiosité mathématique sans réelle application. Dès 1972, Variant souligne l’utilité potentielle de cette loi pour détecter la présence de possibles de fraudes dans des bases de données. L’idée d’utiliser cette loi en comptabilité est apparue à la fin des années 1980 dans un rapport de recherche du chercheur néo-zélandais, Charles Carslaw. Dans les années 1990, l’économiste américain Mark Nigrini popularise l’idée.
Propice à la comptabilité, cette idée peut en fait être extrapolée à d’autres départements comme la Qualité ou le Marketing ; dans un contexte où les données chiffrées sont devenues prépondérantes en entreprise. Des écarts trop importants à la loi peuvent être détectés et présager d’éventuelles erreurs ou fraudes.
Mais concrètement, quels sont les outils existant pour tester la loi de Benford sur vos Data ? Si l’on peut trouver assez facilement des codes en MatLab et Python, leur nature limite l’audience à des personnes plutôt aguerries. Internet étant beaucoup moins prolixe en Excel de qualité, j’ai décidé de développer une solution moi-même. Voici deux fichiers légèrement différents que je partage de manière libre et qui vous permettrons de tester facilement vos données :
Fichiers Excel
Permet de tester sur deux chiffres l’adéquation de vos données par rapport à la loi de Benford et de tracer les histogrammes de fréquence. Il est conseillé d’utiliser des échantillons significatifs de plus de 2000 valeurs.
- La seule limite de taille est celle du nombre de lignes d’Excel un peu supérieure à 1 million.
- L’adéquation à la loi est automatiquement calculée par la loi statistique du Chi-deux (par chiffre et par décimale).
- Un manuel d’utilisation est intégré dans le fichier.
Advanced_Benford_Analysis.xlsm
Reprend les fonctionnalités du fichier précédent avec une analyse plus fine :
- Neuf décimales sont testées au lieu de 2 (en pratique les 4 premières ont un intérêt).
- Possibilité de tester les échantillons par lots avec un rapport détaillé au test d’adéquation du Chi-deux.
- Une fonction benfordProbability permet de calculer la probabilité dans la base de son choix, pour n’importe quelle chiffre et rang de la décimale.
- Le fichier est en anglais et contient un manuel d’utilisation succinct.
- Il est nécessaire d’autoriser les macro (VBA) pour que le code puisse s’exécuter.
Domaines d’application et limites
Le domaine d’application de la loi est crucial et pourtant ce n’est pas évident de le déterminer a priori. Les données les plus candidates à suivre la loi doivent être étalées et régulières avec une taille d’échantillon significatif.
Certains jeux de données ne suivent pas la loi de manière évidente : pas question de tester la loi sur la taille de la population d’un pays car la grande majorité mesure 1.x mètre. De même certaines enseignes pratiquent des prix de la forme x.99€ ce qui peut fausser le résultat sur les décimales. Pour d’autres échantillons c’est plus compliqué. Un bon échantillon de Benford au sens mathématique est engendré par la multiplication entre elles de variables indépendantes [1] ; ce critère n’est malheureusement pas utilisable facilement en pratique. Ce que l’on peut dire c’est que certaines données sont parfaitement en adéquation avec la loi, d’autres tendent vers la loi et d’autres ne fonctionnent pas sans qu’une fraude soit à suspecter.
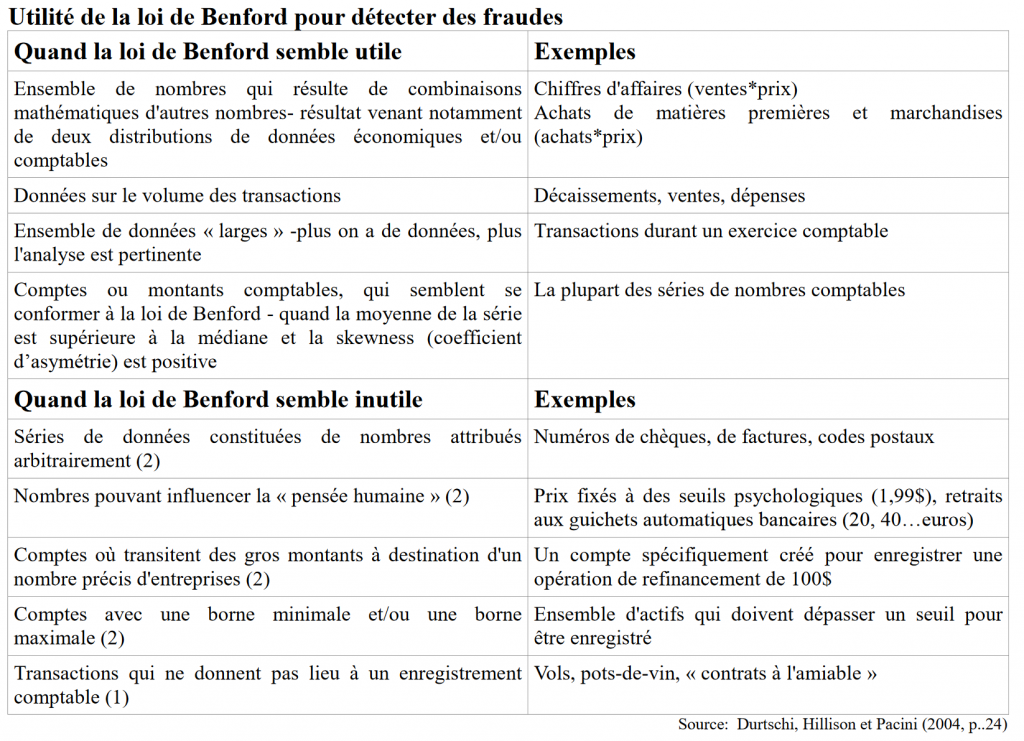
En utilisant les bonnes pratiques du tableau ci-dessous, on écarte déjà certains nombres de cas simples qui ne suivent pas la loi :
Je dirai donc qu’il faut manier la loi avec prudence et garder un esprit critique sur les éventuels « faux positifs ». Des articles détaillés proposent d’autres bonnes pratiques en la matière [2] [3] et les plus aguerris d’entre vous pourrons utiliser d’autres tests statistiques en complément du Chi-deux (test binomial, Kolmogorov-Smirnov etc.) pour affiner l’analyse. Gardez en tête que la loi de Benford est un outil très puissant mais qu’il ne faut pas conclure trop hâtivement si la corrélation du Chi-deux est inférieure à 95%. Des investigations plus poussées doivent être menées lorsqu’un doute apparait.
Conclusion
In theory, practice is the same as theory, but not in practice.
Voilà qui résume bien la situation !
Gardez les yeux bien ouvert sur vos jeux de données 🙂👍🏻
Sources
[1] Nicolas Gauvrit et Jean-Paul Delahaye, Pourquoi la loi de Benford n’est pas mystérieuse (2008)
[2] J.M Pimbley, Benford’s, Law and the Risk of Financial Fraud (2014)
[3] Adrien Bonache, Jonathan Maurice, Karen Moris, Détection de fraudes et loi de Benford : quelques risques associés (2010)